Présentation
Ce cours va tenter de répondre à une question qui vous a peut-être déjà effleuré : comment une machine peut-elle représenter des nombres (entiers -positifs ou négatifs-, réels) ou des caractères ?
Pour répondre à cette question, nous allons devoir (ré)apprendre à compter comme le fait la machine, en rappelant à cette occasion les différentes notions liées aux bases de représentation des nombres. Nous verrons ensuite comment coder les informations de signe et de virgule.
Travail à effectuer
Ces pages sont un mélange de cours et d'exercices. Après avoir lu les paragraphes constituant le cours, une série d'exercices vous sera proposée.. Après avoir répondu à un exercice, un nouvel exercice sera généré (que vous ayez répondu correctement ou non). En cas de réponse incorrecte, la solution vous sera donnée.
Les exercices résolus correctement au moins une fois sont identifiés à l'aide du symbole suivant : ✓
Les exercices qui n'ont pas encore été résolus correctement au moins une fois sont identifiés à l'aide du symbole suivant : ✗
Ces informations étant stockées dans la zone de stockage local du navigateur, elles ne seront pas conservées si vous changez de machine, de compte utilisateur ou de navigateur.
Un peu d'histoire...
Les premiers ordinateurs électroniques sont apparus dans les années 40. Le transistor restant encore à inventer, ils utilisaient des tubes à vide (communément appelés lampes) pour effectuer les opérations demandées. Parmis les plus connus de ces précurseurs, L'ENIAC (1946) comportait 18000 tubes à vide et pesait 30 tonnes pour une capacité de mémoire de 20 nombres de 10 chiffres et une puissance de calcul permettant d'effectuer 5000 opérations par seconde (contre plusieurs milliards sur les ordinateurs modernes). Pour programmer ces "monstres", il fallait manipuler des milliers d'interrupteurs et de câbles et, de temps à autre, remplacer les tubes ayant "grillé" lorsque des insectes commettaient l'erreur (fatale) de vouloir se réchauffer contre eux. |  |
Pour stocker un chiffre décimal (0 à 9), on utilisait alors 10 bascules (composées chacune de 2 lampes), dont une seule à la fois était active :
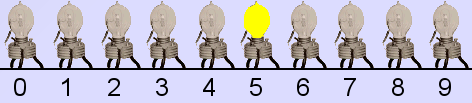
Cette méthode de représentation était assez inefficace, puisque n'utilisant à un moment donné que 10% des ressources dédiées à la mémorisation d'un chiffre. Un autre mode de représentation, déjà utilisé par certains concurrents de l'ENIAC, s'est rapidement imposé : le binaire, autrement dit la représentation en base 2 :

Dans ce mode de représentation, 10 bascules permettent de représenter 1024 valeurs différentes, au lieu de 10 auparavant. Par contre, la base 2 n'est pas naturelle pour l'être humain, habitué à compter en base 10.
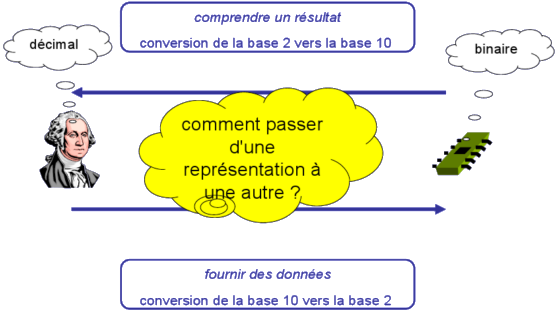
Pour interpréter le résultat d'un calcul, il est donc nécessaire d'en obtenir une représentation en base 10. Inversement, pour fournir des données à un programme, nous préférons la plupart du temps les entrer sous forme décimale. Pour que ces données soient utilisables par un ordinateur travaillant en binaire, une étape de conversion est également nécessaire.
Rappel : bases de représentation des nombres
| base | nom | symboles | exemples |
|---|---|---|---|
| 10 | décimal | 0 1 2 3 4 5 6 7 8 9 | 10295 13,48 |
| 2 | binaire | 0 1 | 101101 101,11 |
| 8 | octal | 0 1 2 3 4 5 6 7 | 724 45,13 |
| 16 | hexadécimal | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 4AC9 B1,D6 |
exemples : (10295)10 (101101)2 (724)8 (4AC9)16
Binaire : base 2
- bit : abréviation de "binary digit" (chiffre binaire)
- Un bit a deux valeurs possibles : 0 ou 1
-› en utilisant plusieurs bits :
- 2 bits : 00, 01, 10, 11 -› 4 combinaisons
- 3 bits : 000, 001, 010, ... -› 8 combinaisons
- 8 bits : 00000000, 00000001, ... -› 256 combinaisons
- etc...
Poids fort / poids faible
Soit C un nombre dont la représentation dans une base b comporte n chiffres notés Cn-1 , Cn-2 , ... , C2 , C1 , C0 :- Cn-1 est appelé chiffre de poids fort de C : c'est le chiffre qui a le plus de poids pour la détermination de la valeur du nombre.
- C0 est appelé chiffre de poids faible de C : c'est le chiffre qui a le moins de poids pour la détermination de la valeur du nombre.